First, let's define some important terminology. An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. Special symbols are used in these statements.
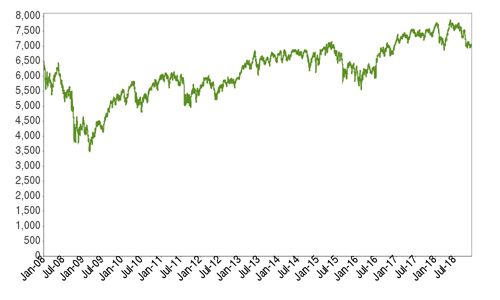
When you read an inequality, read it from left to right—just like reading text on a page. In algebra, inequalities are used to describe large sets of solutions. For example, a set consisting of all even positive integers less than 11 is represented in roster form as and in set-builder form, it is represented as .
The solutions to x\geq 4[/latex] are represented as \left[4,\infty \right)[/latex]. This method is widely used and will be present in other math courses you may take. An interval notation calculator is functioned to write numbers in interval notation. Furthermore, it can be written with rectangular brackets or parentheses, and two numbers that will be enclosed with a comma. These two numbers are known as the endpoints of the interval.
The left number denotes the least element or lower bound. However, if you are using a set builder notation calculator you can have interval notation and set builder notation for any numerical statement simultaneously. For example, the number 5 is an integer, and so it is appropriate to write \(5 \in \mathbb\).
It is not appropriate, however, to write \(5 \subseteq \mathbb\) since 5 is not a set. It is important to distinguish between 5 and . The difference is that 5 is an integer and is a set consisting of one element. Consequently, it is appropriate to write \(\ \subseteq \mathbb\), but it is not appropriate to write \(\ \in \mathbb\).
The distinction between these two symbols is important when we discuss what is called the power set of a given set. Roster notation of a set is a simple mathematical representation of the set in mathematical form. In the roster form, the elements of a set are listed in a row inside the curly brackets. Every two elements are separated by a comma symbol in a roster notation if the set contains more than one element. The roster form is also called the enumeration notation as the enumeration is done one after one.
There are mainly two methods that can be used to represent a set. The Listing method is also called the roster method. This method shows the list of all the elements of a set inside brackets. The elements are written only once and are separated by commas. Roster notation is one of the most simple techniques to represent the elements of a set. A method of listing the elements of a set in a row with comma separation within curly brackets is called the roster notation.
Practice the worksheet on sets in roster form to write a set using the roster or tabular method. We know, to express the set in roster form the elements of a set are listed within the curly brackets and are separated by commas. A method of listing the elements in a row with comma separation within curly brackets is called the roster notation. The above set has only 3 elements, so it would not be difficult to write it in roster form as shown above. However, if your set has hundreds or thousands of elements, it would be hard to list them out, but easy to refer to them using set builder notation.
In Preview Activity \(\PageIndex\), we worked with verbal and symbolic definitions of set operations. However, it is also helpful to have a visual representation of sets. Venn diagrams are used to represent sets by circles drawn inside a rectangle. The points inside the rectangle represent the universal set \(U\), and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure \(\PageIndex\) is a Venn diagram showing two sets.
The contents of a set can be described by listing the elements of the set, separated by commas, inside a set of curly brackets. This way of describing a set is called roster form. It is not actually possible to express all of them in roster form.
Similarly, we don't know the last element in these types of sets. If sets follow a pattern or have a particular sequence, we just write the first three or four elements with a continuous symbol within the curly braces. Use roster notation to create and write two proper subsets of your original set.
Do the following and write your answers in roster notation. N is the set of integers that are greater than or equal to -1 and less than or equal to 2 write the set in roster form. I am really confused on how to do this and what this means over al. please help. An online interval notation calculator helps you to find the interval values from the given set interval notation. Also, this set builder notation calculator allows you to find the set builder notation for the given notation. Apart from set builder & set interval notation, this calculator helps to find total length and topology of the data solution set.
This is best used to represent the sets mainly with an infinite number of elements. It is used commonly with integers, real numbers, and natural numbers. This also is used to represent the sets with intervals and equations. Students have to be very clear and learn precisely so that they can solve any problem related to the topic. Students can refer to Vedantu and learn the chapter clearly with a detailed explanation of every topic. So far we specified the elements of sets by verbally.
The roster form introduced here offers a concise way of writing down sets by listing all elements of the set. Furthermore we use ellipsis to describe the elements in a set, when we believe that the reader understands how a pattern in a list of elements continues. Venn diagrams are visual representations of mathematical sets—or collections of objects—that are studied using a branch of logic called set theory. Set theory is one of the foundational systems for mathematics, and it helped to develop our modern understanding of infinity and real numbers.
Therefore, the existence of the Cartesian product of any two sets in ZFC follows from the axioms of pairing, union, power set, and specification. So simply add some numbers and leave the rest on this set builder notation calculator to have the final outcomes without doing any manual calculations. It is important to remember that these operations on sets produce other sets. Don't confuse these with the symbols from the previous section . \(A \cap B\) is a set, while \(A \subseteq B\) is true or false. This is the same difference as between \(3 + 2\) and \(3 \le 2\) .
In this case only, the roster notation is not recommendable in set theory. The set can be defined by listing all its elements, separated by commas and enclosed within braces. Each object in the set is called an element of the set. If an element x is a member of the set S, we write . If an element x is not a member of the set S, we write . The empty set is the set that contains no elements.
For sets A and B, A is called a subset of B, denoted , if every element of A is also an element of B. When describing ranges in set-builder notation, we could similarly write something like , or if the output had its own variable, we could use it. So for our tree height example above, we could write for the range . Let \(A\) and \(B\) be subsets of a universal set \(U\). For each of the following, draw a Venn diagram for two sets and shade the region that represent the specified set. In addition, describe the set using set builder notation.
Set Builder Notations is the method to describe the set while describing the properties and not just listing its elements. When there is set formation in a set builder notation then it is called comprehension, set an intention, and set abstraction. The roster method is defined as a way to show the elements of a set by listing the elements inside of brackets. List a few elements in the sets below and describe them in words. The set \(\Z\) is the set of integers; positive and negative whole numbers. To learn more about the history of Venn diagrams, read our page answering, "What Is a Venn Diagram?
" Although John Venn popularized representing set theory with overlapping circles, the ideas and symbols in Venn diagrams actually predate him. It is a collection of all elements in a particular context or application. All the sets in that context or application are essentially subsets of this universal set.
The actual problem comes to the roster method with repeated elements in the set. If the elements are few, we can easily express the set in roster form as follows. The roster notation is not comfortable to express many elements in roster form.
The graph then extends endlessly in one direction. This is shown by a line with an arrow at the end. The blue line is drawn to the right on the number line because the values in this area are greater than −3[/latex]. The arrow at the end indicates that the solutions continue infinitely. A Venn diagram is a visual diagram that shows the relationship of sets with one another. The set of all elements being considered is called the universal set and is represented by a rectangle.
Subsets of the universal set are represented by ovals within the rectangle. In the previous examples, we used inequalities to describe the domain and range of the functions. This is one way to describe intervals of input and output values, but is not the only way. If N is the set of natural numbers that are factors of 20, choose the selection below that correctly shows this set in roster form.
I've been so stuck I feel dumb someone help me please.. If N is the set of natural numbers that are factors of 24, choose the selection below that correctly shows this set in roster form. In interval notation method, the starting and the ending number will be represented using the brackets. It has two types of brackets, square bracket and round brackets. If the interval is mentioned in a square bracket, the end values are included.
If the interval is mentioned in round brackets, the end values are not included. Use set builder notation or the roster method to specify the set of integers that are the sum of eight consecutive integers. Use set builder notation or the roster method to specify the set of integers that are the sum of four consecutive integers. Numbers such as real numbers, integers, natural numbers can be easily represented using the set-builder notation.
Also, the set with an interval or equation can be best described by this method. One of the limitations of roster notation is that we cannot represent a large number of data in roster form. For example, if we want to represent the first 100 or 200 natural numbers in a set B then it is hard for us to represent this much data in a single row. This limitation can be overcome by representing data with the help of a dotted line. Take a set of the first 100 positive odd numbers and represent using roster notation.
In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined. In the set builder form, all the elements of the set, must possess a single property to become the member of that set. Researchers and mathematicians have developed a language and system of notation around set theory. If you want to get in on their secrets, you'll want to become familiar with these Venn diagram symbols. The two sets are lengthy and it is not convenient for writing such sets in roster form. Just imagine the roster form of a set if the set contains more than $100$ elements.
It becomes a nightmare for everyone to write it. However, some sets follow a pattern or have a particular sequence. The roster notation is a simple mathematical representation of a set in mathematical form. The set can be defined by describing the elements using mathematical statements.
We need to use set builder notation for the set \(\mathbb\) of all rational numbers, which consists of quotients of integers. The Interval notation is a method to define a set of numbers between a lower limit and an upper limit by using end-point values. The point also has to be remembered that the upper and lower limits may or may not be included in the set. The end values are written between brackets. A square bracket denotes inclusion in the set, while the brackets indicate exclusion from the set. The method of defining a set by describing its properties rather than listing its elements is known as set builder notation.
Recall that an ellipsis (\(\ldots\)) indicates that the pattern is continued. We can use an ellipsis when writing a set in roster form instead of listing every element. Given below are 3 Venn diagrams representing three different sets. Let us represent them in roster form step-wise. Listing the elements of a set inside a pair of braces is called the roster form. ☐ Express the union or intersection of sets of numbers in interval notation.
Set In Roster Form Calculator RestaurantABCMcDonald'sXXWendy'sXXBurger KingIn-N-OutXXTaco BellXXKFCA&WChick-fil-AXXXNow it's time to create a Venn diagram representing the results. It uses the symbol we explained, ∩, to show the intersection between two and three sets. There are eight regions that our restaurants could occupy. The set is represented by listing all the elements comprising it.